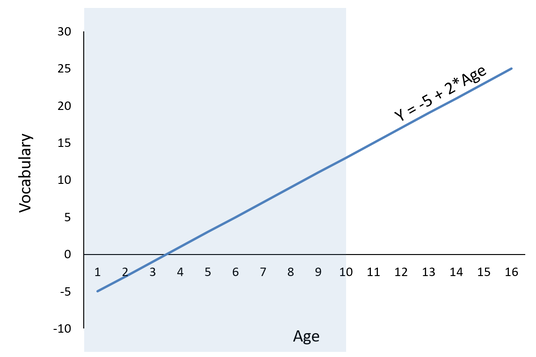
I'm teaching regression right now and a question that comes up a lot is how an intercept can be negative when the outcome has a range of scores of something like a grade on a vocabulary test in percent correct (0-100%). Worse, sometimes the regression suggests that the negative intercept is significantly different from zero! Can we really conclude that there are people who got a negative score on a vocabulary test? 

Regression is based around the idea of model comparisons; where models with added predictors are compared to an unconditional model (a model with no predictors) to determine if better fit has been achieved. In the unconditional model, each person’s observed score on the Y (the outcome) is always equal to the mean of Y (represented as B0) plus error: 

  Y = B0 + e 

Because B0 is equal to the mean of Y, in our hypothetical example of percentage correct on a final test, the intercept will never be negative. It could be really small if your class of students absolutely bombed their test, but it won't ever be negative.  But we don't really ever interpret unconditional models. In a regression, you will always have at least one predictor. We add a predictor in an attempt to make the error smaller. In other words, we attempt to explain more of the error, and better fit the observed data points.

So let's suppose that my vocabulary test is completed by 200 students, aged 10-15. I generally expect that older children will have larger vocabularies (and thus, higher scores on this vocabulary test). When we add a predictor to this equation, it is now a conditional model. In regression, the conditional model predicting vocabulary from age will look like this:

 Y = B0 + B1*age + e 

Where Y = the expected vocabulary score for someone who is zero years old. Why for someone who is zero? Because if the x-value plugged in for age is zero, then the weight (B1) is reduced to zero, and so Y = B0. The key phrase here is “someone who is zero years old” because it is what makes the expected score of Y conditional. The expected value of Y (and so the estimate of B0, which is also called the Y-intercept or often just “intercept”) is always equal to the mean of Y when all predictors are zero.

So in our hypothetical example, our age variable ranges from 10-16, and so does not include zero. If the age coefficient is significantly positive, there's a strong possibility that the intercept may be negative. Inventing some results, I graphed them at the right: With the equation Y = -5 + 2* Age. 

Here I've estimated that a 10 year old has an expected vocabulary score of 15, and that every year age increase corresponds to an expected 2 point increase in vocabulary score. That means we have a negative intercept (B0 = -5).  The negative intercept is completely possible, because we are trying to estimate the vocabulary score of... a newborn baby. The whole shaded part of that figure represents a place on the distribution where we don't have any data. 

So. Only interpret your intercept, negative or not, when the zero point lies within the observed range of your data. If it doesn't, you have two choices. 1) Don't interpret it, just ignore it. or 2) re-center your predictors so that they all do contain your zero point, and now you can interpret the intercept. What's centering? We'll do that another day. 

​In his post “data analysis is thinking, data analysis is theorizing” Sanjay Srivastava touches on several topics that resonated with my sense of the importance of the work that my colleagues and I do in the field of methodology. Sanjay discusses the Many Analysts, One Dataset study, which found that even with the same dataset and same hypotheses, different analysts came to different statistical conclusions. Sanjay states: “the variability was neither statistical noise nor human error. Rather the differences in results were because of different reasoned decisions by experienced data analysts” This well-articulated point highlights some of the important theoretical work that is done by statisticians and methodologists. It also highlights what I believe is so wrong and broken in the relationship between content researchers (what I am using to refer to those researchers who primarily study an academic area such as personality, family relationships, or poverty) and statisticians or data analysts.
 
An applied statistician is essentially always working outside of their area of expertise. Working outside of your area of expertise is not fun and is not easy. Imagine if to get your summer salary covered you were asked to write two papers in a completely new field. Do you study social psychology? Congratulations, this summer you’ve been assigned to collect data and write two papers about the diversity of insect species in the wetlands of Florida. It’s ludicrous. You wouldn’t even know where to start. This is similar to what you ask statisticians to do when they are involved in a project at the last minute. You essentially say: “Here’s an area of work I’ve spent the last 10 years of my life thinking about, can you tell me if my intervention works by the end of the month?”.  Yes, I absolutely can, but if this is the first time you’ve talked to me, I can pretty much guarantee you’re not going to like my answer. All of the underlying groundwork; hundreds of methodological choices have been made without my input. Making decisions at this point is the equivalent of dropping me in a Florida wetland to count bugs. I am going to do it wrong; make the wrong choices, otherwise invalidate your best intentions.
 
My goal here is not to scare you. Rather my goal is to encourage you. To tell you that science can be better. That you can get closer to answering the questions you really want to answer with a little more forethought. When you want to design a study, you should reach out to someone with expertise in how to design a study. My call to content researchers is to consider the methodologist as a research partner with an area of expertise, and not as someone who can provide some last minute help to run a model. Statisticians will make the wrong choices, and will analyze your data wrong if they don’t understand the underlying theories behind what you’re trying to do, and what new knowledge you’re trying to bring into the world. 

When you are designing a quantitative study, you need to consider the potential power you have to detect effects. Any power analysis you run will have four components:

1. Alpha (how often are you OK with thinking there's an effect there when there actually isn't? Typically in developmental science these are set at .05; or 5% of the time)
   
2. Beta (How often are you OK with missing an effect that might actually be there? Usually we say 20% of the time: Power is 1- that probability, so  .80) 
   
3. Sample Size (number of people)
   
4. Effect size (how big can you expect the difference or relation you are looking for to be?)

These four components are all parts of the same equation: If you know three of these then you can always predict the fourth. Just like an equation like 3 = X + 1, you create one degree of freedom when you leave one of those four elements blank. That means you can use a power analysis to either pick how much power you have, how many people you need, or how big of an effect you can detect. 

In education,we also often need to consider multiple factors like how the data are structured, like how random assignment occurred (if it's happening at all), or whether kids are nested in classrooms. These factors add additional elements to these equations. In this powerpoint presentation, I go over some of the features of how to calculate a power analysis when you're planning education research.